Glauber–Sudarshan P-representation
The Glauber-Sudarshan P-representation is a suggested way of writing down the state of any type of light using the coherent states as a basis. It was developed by George Sudarshan and later adopted by Roy J. Glauber (see the references below). It was the subject of a controversy when Glauber was awarded a share of the 2005 Nobel Prize in Physics for his work in this field and George Sudarshan's contribution was not recognized.
In this representation, the density matrix 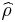 is written as:
is written as:
where 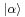 are the coherent states and
are the coherent states and 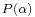 is a quasi-probability distribution.
is a quasi-probability distribution.
The matter is not quite simple. According to Mandel and Wolf: "The different coherent states are not [mutually] orthogonal, so that even if 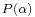 behaved like a true probability density [function], it would not describe probabilities of mutually exclusive states."[1]
behaved like a true probability density [function], it would not describe probabilities of mutually exclusive states."[1]
Contents |
References
Citations
- ^ Mandel & Wolf 1995, p. 541
Citation bibliography
Mandel, L.; Wolf, E. (1995), Optical Coherence and Quantum Optics, Cambridge UK: Cambridge University Press, ISBN 0-521-41711-2
General references
- E. C. G. Sudarshan, Phys. Rev. Letters 10, 277 (1963)
- Roy J. Glauber, Physical Review 131, 2766 (1963)
